|
|
3.3.3 Term orderings
Any polynomial (resp. vector) in SINGULAR is ordered w.r.t. a
term ordering (or, monomial ordering), which has to be specified
together with the declaration of a ring. SINGULAR stores and
displays a polynomial (resp. vector) w.r.t. this ordering, i.e., the
greatest monomial (also called the leading monomial) is the first one
appearing in the output polynomial, and the smallest monomial is the last one.
Remark: The novice user should generally use the ordering
dp for computations in the polynomial ring
![$K[x_1,\ldots,x_n]$](sing_60.png) ,resp. ,resp. ds for computations in the localization
![$\hbox{Loc}_{(x)}K[x_1,\ldots,x_n])$](sing_61.png) .For more details, see Polynomial data. .For more details, see Polynomial data.
In a ring declaration, SINGULAR offers the following orderings:
- Global orderings
lp
- lexicographical ordering
rp
- reverse lexicographical ordering, i.e. a lexicographical ordering from the right
with 1 < x_1 < ... <x_n
(should not be used as it reverses the "natural" x_1 > ... > x_n,
reorder the variables instead)
dp
- degree reverse lexicographical ordering
Dp
- degree lexicographical ordering
wp( intvec_expression )
- weighted reverse lexicographical ordering; the weight vector is expected to
consist of positive integers only.
Wp( intvec_expression )
- weighted lexicographical ordering; the weight vector is expected to consist of
positive integers only.
Global orderings are well-orderings, i.e.,
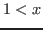 for each ring
variable for each ring
variable
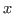 . They are denoted by a . They are denoted by a p as the second
character in their name.
- Local orderings
ls
- negative lexicographical ordering
rs
- negative reverse lexicographical ordering, i.e. a lexicographical ordering from the right
(should not be used as it reverses the "natural" x_1 < ... < x_n,
reorder the variables instead)
ds
- negative degree reverse lexicographical ordering
Ds
- negative degree lexicographical ordering
ws( intvec_expression )
- (general) weighted reverse lexicographical ordering; the first element
of the weight vector has to be non-zero.
Ws( intvec_expression )
- (general) weighted lexicographical ordering; the first element
of the weight vector has to be non-zero.
Local orderings are not well-orderings. They are denoted by an s
as the second character in their name.
- Matrix orderings
M( intmat_expression )
- intmat_expression has to be an invertible square matrix
Using matrix orderings, SINGULAR can compute standard bases
w.r.t. any monomial ordering which is compatible with the natural
semi-group structure on the monomials. In practice, the predefined global
and local orderings together with the block orderings should be
sufficient in most cases. These orderings are faster than their
corresponding matrix orderings since evaluation of a matrix ordering is more
time consuming.
- Extra weight vector
a( intvec_expression )
- an extra weight vector
a( intvec_expression ) may precede
any monomial ordering
- Product ordering
( ordering [ ( int_expression ) ], ... )
- any of the above orderings and the extra weight vector may be combined
to yield product or block orderings
The orderings lp, dp, Dp, ls, ds,
Ds and rp may be followed by an int_expression in
parentheses giving the
size of the block. For the last block the size is calculated
automatically. For weighted orderings, the size of the block is given
by the size of the weight vector. The same holds analogously for matrix
orderings.
- Module orderings
( ordering, ..., C )
( ordering, ..., c )
- sort polynomial vectors by the monomial ordering first, then by
components
( C, ordering, ... )
( c, ordering, ... )
- sort polynomial vectors by components first, then by the monomial
ordering
Here a capital C sorts generators in ascending order, i.e.,
gen(1) < gen(2) < .... A small c sorts in
descending order, i.e., gen(1) > gen(2) > .... It is
not necessary to specify the module ordering explicitly since (
ordering, ..., C ) is the default.
In fact, c or C may be specified anywhere in a product
ordering specification, not only at its beginning or end. All monomial
block orderings preceding the component ordering have higher precedence,
all monomial block orderings following after it have lower precedence.
For a mathematical description of these orderings, see
Polynomial data.
|
 Online Manual
Online Manual