|
|
C.3 Syzygies and resolutions
Syzygies
Let  be a quotient of be a quotient of
![$\hbox{Loc}_< K[\underline{x}]$](sing_656.png) and let and let
 be a submodule of be a submodule of  .
Then the module of syzygies (or 1st syzygy module, module of relations) of .
Then the module of syzygies (or 1st syzygy module, module of relations) of  , syz( , syz( ), is defined to be the kernel of the map ), is defined to be the kernel of the map
 . .
The k-th syzygy module is defined inductively to be the module
of syzygies of the
 -stsyzygy module. -stsyzygy module.
Note, that the syzygy modules of  depend on a choice of generators depend on a choice of generators  .
But one can show that they depend on .
But one can show that they depend on  uniquely up to direct summands. uniquely up to direct summands.
Example:
| | ring R= 0,(u,v,x,y,z),dp;
ideal i=ux, vx, uy, vy;
print(syz(i));
==> -y,0, -v,0,
==> 0, -y,u, 0,
==> x, 0, 0, -v,
==> 0, x, 0, u
|
Free resolutions
Let
 and and  .
A free resolution of .
A free resolution of  is a long exact sequence is a long exact sequence
where the columns of the matrix
 generate generate
 . Note that resolutions need not to be finite (i.e., of
finite length). The Hilbert Syzygy Theorem states that for . Note that resolutions need not to be finite (i.e., of
finite length). The Hilbert Syzygy Theorem states that for
![$R = \hbox{Loc}_< K[\underline{x}]$](sing_620.png) there exists a ("minimal") resolution of length not exceeding the number of
variables. there exists a ("minimal") resolution of length not exceeding the number of
variables.
Example:
| | ring R= 0,(u,v,x,y,z),dp;
ideal I = ux, vx, uy, vy;
resolution resI = mres(I,0); resI;
==> 1 4 4 1
==> R <-- R <-- R <-- R
==>
==> 0 1 2 3
==>
// The matrix A_1 is given by
print(matrix(resI[1]));
==> vy,uy,vx,ux
// We see that the columns of A_1 generate I.
// The matrix A_2 is given by
print(matrix(resI[3]));
==> u,
==> -v,
==> -x,
==> y
|
Betti numbers and regularity
Let  be a graded ring (e.g., be a graded ring (e.g.,
![$R = \hbox{Loc}_< K[\underline{x}]$](sing_620.png) ) and
let ) and
let  be a graded submodule. Let be a graded submodule. Let
be a minimal free resolution of  considered with homogeneous maps
of degree 0. Then the graded Betti number considered with homogeneous maps
of degree 0. Then the graded Betti number  of of  is
the minimal number of generators is
the minimal number of generators  in degree in degree  of the of the 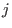 -th
syzygy module of -th
syzygy module of  (i.e., the (i.e., the  -st syzygy module of -st syzygy module of
 ). Note that, by definition, the ). Note that, by definition, the  -th syzygy module of -th syzygy module of  is is  and the 1st syzygy module of
and the 1st syzygy module of  is is  . .
The regularity of
 is the smallest integer is the smallest integer
 such that such that
Example:
| | ring R= 0,(u,v,x,y,z),dp;
ideal I = ux, vx, uy, vy;
resolution resI = mres(I,0); resI;
==> 1 4 4 1
==> R <-- R <-- R <-- R
==>
==> 0 1 2 3
==>
// the betti number:
print(betti(resI), "betti");
==> 0 1 2 3
==> ------------------------------
==> 0: 1 - - -
==> 1: - 4 4 1
==> ------------------------------
==> total: 1 4 4 1
==>
// the regularity:
regularity(resI);
==> 2
|
|