|
|
C.4 Characteristic sets
Let 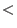 be the lexicographical ordering on be the lexicographical ordering on
![$R=K[x_1,...,x_n]$](sing_671.png) with with
 .
For .
For  let lvar( let lvar( ) (the leading variable of ) (the leading variable of  ) be the largest
variable in ) be the largest
variable in  ,
i.e., if ,
i.e., if
 for some for some
 then lvar then lvar . .
Moreover, let
ini
 . The pseudoremainder . The pseudoremainder
 of of  with respect to with respect to  is
defined by the equality is
defined by the equality
 with with
 and and 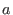 minimal.
minimal.
A set
 is called triangular if is called triangular if
 . Moreover, let . Moreover, let  ,
then ,
then  is called a triangular system, if is called a triangular system, if  is a triangular set
such that is a triangular set
such that  does not vanish on does not vanish on
 . .
 is called irreducible if for every is called irreducible if for every  there are no there are no
 , , , , such that such that
Furthermore,  is called irreducible if is called irreducible if  is irreducible. is irreducible.
The main result on triangular sets is the following: Let
 , then there are irreducible triangular sets , then there are irreducible triangular sets  such that
such that
 where
where
 . Such a set . Such a set
 is called an irreducible characteristic series of
the ideal is called an irreducible characteristic series of
the ideal  . .
Example:
| | ring R= 0,(x,y,z,u),dp;
ideal i=-3zu+y2-2x+2,
-3x2u-4yz-6xz+2y2+3xy,
-3z2u-xu+y2z+y;
print(char_series(i));
==> _[1,1],3x2z-y2+2yz,3x2u-3xy-2y2+2yu,
==> x, -y+2z, -2y2+3yu-4
|
|