|
|
A.3.6 Computation of Ext
We start by showing how to calculate the n-th Ext group of an ideal. The
ingredients to do this are by the definition of Ext the following:
calculate a (minimal) resolution at least up to length n, apply the Hom
functor, and calculate the n-th homology group, that is, form the
quotient ker/im in the resolution sequence.
The Hom functor is given simply by transposing (hence dualizing) the
module or the corresponding matrix with the command transpose.
The image of the (n-1)-st map is generated by the columns of the
corresponding matrix. To calculate the kernel apply the command
syz at the (n-1)-st transposed entry of the resolution.
Finally, the quotient is obtained by the command modulo, which
gives for two modules A = ker, B = Im the module of relations of
in the usual way. As we have a chain complex, this is obviously the same
as ker/Im.
We collect these statements in the following short procedure:
| | proc ext(int n, ideal I)
{
resolution rs = mres(I,n+1);
module tAn = transpose(rs[n+1]);
module tAn_1 = transpose(rs[n]);
module ext_n = modulo(syz(tAn),tAn_1);
return(ext_n);
}
|
Now consider the following example:
| | ring r5 = 32003,(a,b,c,d,e),dp;
ideal I = a2b2+ab2c+b2cd, a2c2+ac2d+c2de,a2d2+ad2e+bd2e,a2e2+abe2+bce2;
print(ext(2,I));
==> 1,0,0,0,0,0,0,
==> 0,1,0,0,0,0,0,
==> 0,0,1,0,0,0,0,
==> 0,0,0,1,0,0,0,
==> 0,0,0,0,1,0,0,
==> 0,0,0,0,0,1,0,
==> 0,0,0,0,0,0,1
ext(3,I); // too big to be displayed here
|
The library homolog.lib contains several procedures for computing
Ext-modules and related modules, which are much more general and
sophisticated than the above one. They are used in the following
example:
If
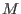 is a module, then is a module, then
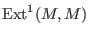 , resp. , resp.
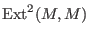 ,are the modules of infinitesimal deformations, respectively of obstructions,
of ,are the modules of infinitesimal deformations, respectively of obstructions,
of
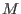 (like T1 and T2 for a singularity). Similar to the treatment of
singularities, the semiuniversal deformation of (like T1 and T2 for a singularity). Similar to the treatment of
singularities, the semiuniversal deformation of
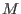 can be computed (if can be computed (if
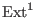 is finite dimensional) with the help of is finite dimensional) with the help of
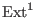 , , 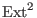 and the cup product.
There is an extra procedure for and the cup product.
There is an extra procedure for
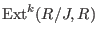 if if
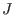 is an ideal in is an ideal in
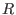 , since this is faster than the
general Ext. , since this is faster than the
general Ext.
We compute
-
the infinitesimal deformations
(
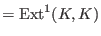 )and obstructions
( )and obstructions
(
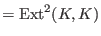 )of the residue field )of the residue field
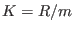 of an ordinary cusp, of an ordinary cusp,
![$R=K[x,y]_m/(x^2-y^3)$](sing_429.png) , , 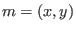 .To compute .To compute
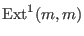 we have to apply we have to apply Ext(1,syz(m),syz(m)) with
syz(m) the first syzygy module of
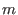 , which is isomorphic to , which is isomorphic to
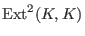 . . -
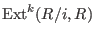 for some ideal for some ideal
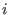 and with an extra option. and with an extra option.
| | LIB "homolog.lib";
ring R=0,(x,y),ds;
ideal i=x2-y3;
qring q = std(i); // defines the quotient ring k[x,y]_m/(x2-y3)
ideal m = maxideal(1);
module T1K = Ext(1,m,m); // computes Ext^1(R/m,R/m)
==> // dimension of Ext^1: 0
==> // vdim of Ext^1: 2
==>
print(T1K);
==> 0,x,0,y,
==> x,0,y,0
printlevel=2; // gives more explanation
module T2K=Ext(2,m,m); // computes Ext^2(R/m,R/m)
==> // Computing Ext^2 (help Ext; gives an explanation):
==> // Let 0<--coker(M)<--F0<--F1<--F2<--... be a resolution of coker(M),
==> // and 0<--coker(N)<--G0<--G1 a presentation of coker(N),
==> // then Hom(F2,G0)-->Hom(F3,G0) is given by:
==> y2,x,
==> x, y
==> // and Hom(F1,G0) + Hom(F2,G1)-->Hom(F2,G0) is given by:
==> -y,x, x,0,y,0,
==> x, -y2,0,x,0,y
==>
==> // dimension of Ext^2: 0
==> // vdim of Ext^2: 2
==>
print(std(T2K));
==> 0,x,0,y,
==> x,0,y,0
printlevel=0;
module E = Ext(1,syz(m),syz(m));
==> // dimension of Ext^1: 0
==> // vdim of Ext^1: 2
==>
print(std(E));
==> x, 0,-y2,x,0,y,
==> -y,0,x, 0,y,0,
==> 0, 1,0, 0,0,0,
==> 1, 0,0, 0,0,0
//The matrices which we have just computed are presentation matrices
//of the modules T2K and E. Hence we may ignore those columns
//containing 1 as an entry and see that T2K and E are isomorphic
//as expected, but differently presented.
//-------------------------------------------
ring S=0,(x,y,z),dp;
ideal i = x2y,y2z,z3x;
module E = Ext_R(2,i);
==> // dimension of Ext^2: 1
==>
print(E);
==> 0,y,0,z2,
==> z,0,0,-x,
==> 0,0,x,-y
// if a 3-rd argument of type int is given,
// a list of Ext^k(R/i,R), a SB of Ext^k(R/i,R) and a vector space basis
// is returned:
list LE = Ext_R(3,i,0);
==> // dimension of Ext^3: 0
==> // vdim of Ext^3: 2
==>
LE;
==> [1]:
==> _[1]=y*gen(1)
==> _[2]=x*gen(1)
==> _[3]=z2*gen(1)
==> [2]:
==> _[1]=y*gen(1)
==> _[2]=x*gen(1)
==> _[3]=z2*gen(1)
==> [3]:
==> _[1,1]=z
==> _[1,2]=1
print(LE[2]);
==> y,x,z2
print(kbase(LE[2]));
==> z,1
|
|