|
|
A.3.7 Depth
We compute the depth of the module of Kaehler differentials
D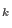 (R)of the variety defined by the (R)of the variety defined by the
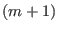 -minors of a generic symmetric -minors of a generic symmetric
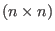 -matrix.We do this by computing the resolution over the polynomial
ring. Then, by the Auslander-Buchsbaum formula, the depth is equal to
the number of variables minus the length of a minimal resolution. This
example was suggested by U. Vetter in order to check whether his bound -matrix.We do this by computing the resolution over the polynomial
ring. Then, by the Auslander-Buchsbaum formula, the depth is equal to
the number of variables minus the length of a minimal resolution. This
example was suggested by U. Vetter in order to check whether his bound
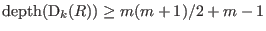 could be improved. could be improved.
| | LIB "matrix.lib"; LIB "sing.lib";
int n = 4;
int m = 3;
int N = n*(n+1) div 2; // will become number of variables
ring R = 32003,x(1..N),dp;
matrix X = symmat(n); // proc from matrix.lib
// creates the symmetric generic nxn matrix
print(X);
==> x(1),x(2),x(3),x(4),
==> x(2),x(5),x(6),x(7),
==> x(3),x(6),x(8),x(9),
==> x(4),x(7),x(9),x(10)
ideal J = minor(X,m);
J=std(J);
// Kaehler differentials D_k(R)
// of R=k[x1..xn]/J:
module D = J*freemodule(N)+transpose(jacob(J));
ncols(D);
==> 110
nrows(D);
==> 10
//
// Note: D is a submodule with 110 generators of a free module
// of rank 10 over a polynomial ring in 10 variables.
// Compute a full resolution of D with sres.
// This takes about 17 sec on a Mac PB 520c and 2 sec an a HP 735
int time = timer;
module sD = std(D);
list Dres = sres(sD,0); // the full resolution
timer-time; // time used for std + sres
==> 0
intmat B = betti(Dres);
print(B,"betti");
==> 0 1 2 3 4 5 6
==> ------------------------------------------------
==> 0: 10 - - - - - -
==> 1: - 10 - - - - -
==> 2: - 84 144 60 - - -
==> 3: - - 35 80 60 16 1
==> ------------------------------------------------
==> total: 10 94 179 140 60 16 1
==>
N-ncols(B)+1; // the desired depth
==> 4
|
|