|
|
C.8.1 Codes and the decoding problem
Codes
-
Let
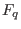 be a field with be a field with 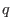 elements. A linear code elements. A linear code 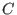 is a linear subspace of is a linear subspace of 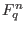 endowed with the
Hamming metric. endowed with the
Hamming metric. -
Hamming distance between x,y
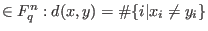 .
Hamming weight of x .
Hamming weight of x
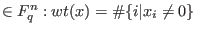 . . -
Minimum distance of the code
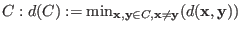 . . -
The code
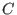 of dimension of dimension 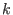 and minimum distance and minimum distance 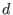 is denoted as is denoted as ![$[n,k,d]$](sing_766.png) . . -
A matrix
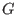 whose rows are the base vectors of whose rows are the base vectors of 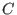 is the generator matrix. is the generator matrix. -
A matrix
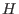 with the property with the property
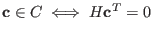 is the check matrix. is the check matrix.
Cyclic codes
The code 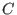 is cyclic, if for every codeword is cyclic, if for every codeword
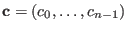 in in 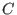 its
cyclic shift its
cyclic shift
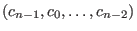 is again a codeword in is again a codeword in 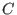 .
When working with cyclic codes, vectors are usually presented as polynomials.
So .
When working with cyclic codes, vectors are usually presented as polynomials.
So 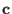 is represented by the polynomial is represented by the polynomial
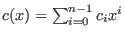 with with 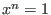 , more
precisely , more
precisely 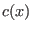 is an element of the factor ring is an element of the factor ring
![$F_q[X]/\langle X^n-1 \rangle$](sing_775.png) .
Cyclic codes over .
Cyclic codes over 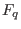 of length of length 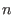 correspond one-to-one to ideals in this factor ring.
We assume for cyclic codes that correspond one-to-one to ideals in this factor ring.
We assume for cyclic codes that 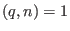 . Let . Let 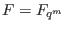 be
the splitting field of be
the splitting field of 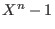 over over 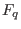 . Then . Then 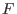 has a primitive has a primitive 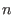 -th root of unity which will be denoted by -th root of unity which will be denoted by 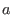 .
A cyclic code is uniquely given by a defining set .
A cyclic code is uniquely given by a defining set 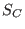 which is a subset of which is a subset of 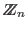 such that such that
A cyclic code has several defining sets.
Decoding problem
-
Complete decoding: Given
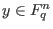 and a code and a code
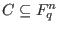 , so that , so that 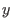 is at distance is at distance 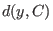 from
the code, find from
the code, find
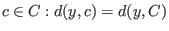 . . -
Bounded up to half the minimum distance: With the additional assumption
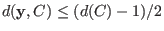 , a codeword with the above property
is unique. , a codeword with the above property
is unique.
Decoding via systems solving
One distinguishes between two concepts:
-
Generic decoding: Solve some system
 and obtain some "closed" formulas and obtain some "closed" formulas 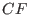 . Evaluating these formulas
at data specific to a received word . Evaluating these formulas
at data specific to a received word 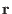 should yield a solution to the decoding problem. For example for should yield a solution to the decoding problem. For example for
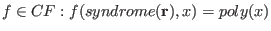 . The roots of . The roots of 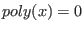 yield error positions, see the section on the
general error-locator polynomial. yield error positions, see the section on the
general error-locator polynomial. -
Online decoding: Solve some system
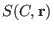 . The solutions should solve the decoding problem. . The solutions should solve the decoding problem.
Computational effort
- Generic decoding. Here, preprocessing is very hard, whereas decoding is relatively simple (if the formulas are sparse).
- Online decoding. In this case, decoding is the hard part.
|