|
|
C.8.2 Cooper philosophy
Computing syndromes in cyclic code case
Let 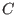 be an be an ![$[n,k]$](sing_793.png) cyclic code over cyclic code over 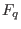 ; ; 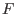 is a splitting field with is a splitting field with 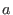 being a primitive n-th root of unity. Let being a primitive n-th root of unity. Let
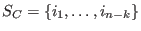 be the complete defining set of be the complete defining set of 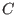 . Let . Let
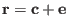 be a received word with
be a received word with 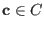 and and 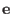 an error vector.
Denote the corresponding polynomials in an error vector.
Denote the corresponding polynomials in
![$F_q[x]/\langle x^n-1 \rangle$](sing_798.png) by by 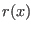 , , 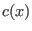 and and  , resp. Compute syndromes , resp. Compute syndromes
where 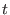 is the number of errors, is the number of errors, 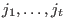 are the error positions and are the error positions and
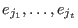 are the error values. Define are the error values. Define 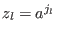 and and 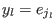 . Then . Then 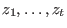 are the error locations and are the error locations and 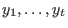 are the error values and
the syndromes above become generalized power sum functions are the error values and
the syndromes above become generalized power sum functions
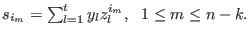
CRHT-ideal
Replace the concrete values above by variables and add some natural restrictions. Introduce
-
 ; ; -
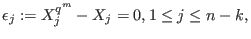 since since 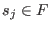 ; ; -
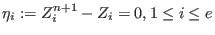 , since , since 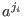 are either are either 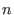 -th roots of unity or zero; -th roots of unity or zero; -
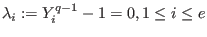 , since , since
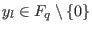 . .
We obtain the following set of polynomials in the variables
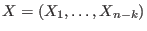 , ,
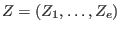 and and
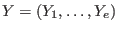 : :
The zero-dimensional ideal 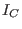 generated by generated by 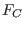 is the CRHT-syndrome ideal
associated to the code is the CRHT-syndrome ideal
associated to the code 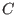 , and the variety , and the variety 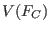 defined by defined by 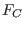 is the CRHT-syndrome variety,
after Chen, Reed, Helleseth and Truong. is the CRHT-syndrome variety,
after Chen, Reed, Helleseth and Truong.
General error-locator polynomial
Adding some more polynomials to 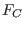 , thus obtaining some , thus obtaining some 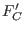 , it is possible to prove the following Theorem: , it is possible to prove the following Theorem:
Every cyclic code 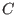 possesses a general error-locator polynomial possesses a general error-locator polynomial  from from
![$F_q[X_1,\ldots ,X_{n-k},Z]$](sing_825.png) that satisfies the following
two properties: that satisfies the following
two properties:
-
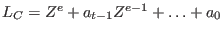 with with
![$a_j\in F_q[X_1,\dots ,X_{n-k}],\ 0\le j\le e-1$](sing_827.png) , where , where 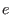 is the error-correcting
capacity; is the error-correcting
capacity; -
given a syndrome
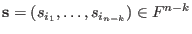 corresponding to an error of weight corresponding to an error of weight 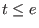 and error locations
and error locations
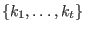 , if we evaluate the , if we evaluate the 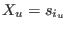 for all for all
 ,
then the roots of ,
then the roots of
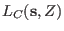 are exactly are exactly
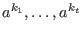 and 0 of multiplicity and 0 of multiplicity 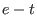 , in other words , in other words
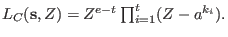
The general error-locator polynomial actually is an element of the reduced Gröbner basis of
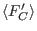 . Having this polynomial,
decoding of the cyclic code . Having this polynomial,
decoding of the cyclic code 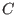 reduces to univariate factorization. reduces to univariate factorization.
For an example see sysCRHT in decodegb_lib.
More on Cooper's philosophy and the general error-locator polynomial can be found in [OS2005].
Finding the minimum distance
The method described above can be adapted to find the minimum distance of a code.
More concretely, the following holds:
Let 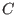 be the binary be the binary ![$[n,k,d]$](sing_766.png) cyclic code with the defining set cyclic code with the defining set
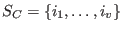 . Let . Let 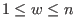 and let and let 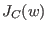 denote the system: denote the system:
Then the number of solutions of 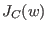 is equal to is equal to 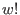 times the number of codewords of weight times the number of codewords of weight 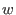 . And for . And for 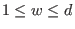 , either , either 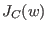 has no solutions, which is equivalent to
has no solutions, which is equivalent to 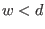 , or , or 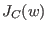 has some solutions, which is equivalent to has some solutions, which is equivalent to 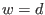 . .
For an example see sysCRHTMindist in decodegb_lib.
More on finding the minimum distance with Groebner bases can be found in [S2007].
See [OS2005], for the definition of the polynomial
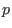 above. above.
|
 Online Manual
Online Manual