Singular

7.7.1 Examples of use of LETTERPLACE

First, define a commutative ring in SINGULAR, equipped with a monomial well-ordering and call it, say, r.

Then, decide what should be the degree (length) bound 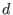, that is how long may the words (monomials in the free algebra) become and run the procedure freeAlgebra(r, d).

This procedure creates a commutative Letterplace ring with an ordering, corresponding to the one in the original commutative ring , see Monomial orderings on free algebras.

In this 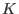-algebra, define an ideal I as a list of polynomials in the free algebra (x*y and y*x are different) and run, for example, twostd (letterplace). The answer is a two-sided Groebner bases of the two-sided ideal 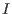. Then, we want to compute the two-sided normal form of xyzy with respect to J with the function reduce.

We illustrate the approach with the following example:

LIB "freegb.lib";
ring r = 0,(x,y,z),dp;
def R = freeAlgebra(r, 4);  // degree (length) bound 4; the ordering will be degree right lex
setring R;
ideal I = x*y + y*z, x*x + x*y - z; // a non-graded ideal
ideal J = twostd(I);
J;
==> J[1]=x*y+y*z
==> J[2]=x*x-y*z-z
==> J[3]=y*z*y-y*z*z+z*y
==> J[4]=y*z*x+y*z*z+z*x-x*z
==> J[5]=y*z*z*y-y*z*z*z-x*z*y
==> J[6]=y*z*z*x+y*z*z*z-x*z*x+y*z*z+z*z
poly p = reduce(x*y*z*y,J);
p; // since p!=0, x*y*z*y is not contained in J
==> -y*z*z*z-x*z*y
qring Q = J;
poly p = reduce(x*x, twostd(0)); // the canonical representative of x*x in Q
p;	
==> y*z+z
rightstd(ideal(p)); // right Groebner basis of the right ideal, generated by p in Q
==> _[1]=z*z
==> _[2]=y*z+z
==> _[3]=x*z

There are various conversion routines in the library freegb_lib (see freegb_lib). Many algebras are predefined in the library fpalgebras_lib (see fpalgebras_lib). Important ring-theoretic properties can be established with the help of the library fpaprops_lib (see fpaprops_lib), while K-dimension and monomial bases and Hilbert data - with the help of the library fpadim_lib (see fpadim_lib). We work further on implementing more algorithms for non-commutative ideals and modules over free associative algebra.